9616. Анти палиндромные строки

Даны два числа n и m. Посчитайте количество строк длины n, символы которых принадлежат алфавиту размера m, которые не содержат в качестве подстроки палиндромов длины больше единицы.

Вход. В первой строке записано целое число t – количество тестов. Каждый тест представляет собой строку, в которой записано два целых числа n и m (1 ≤ n, m ≤ 10⁹).

Выход. Для каждого теста выведите требуемое количество по модулю 10⁹ + 7.

Пример входа	Пример выхода
2 5 6 6 5	1920 1620

РЕШЕНИЕ

степень

Анализ алгоритма

Если строка не содержат в себе подстроку – палиндром длины 2 или длины 3, то она и не содержат в себе подстроку – палиндром длины больше единицы.

Если n = 1, то строка длины 1 может содержать любую из m букв. Искомое число строк равно m.

Если m = 1 и n > 1, то ответ 0, так как имеется единственная строка aa..aa и она содержит палиндром aa.

Если n = 2, то на первой позиции строки может находиться любая из m букв, а на второй позиции – любая из m – 1 букв (буквы в первой и второй позиции не должны совпадать, образуя палиндром). Количество искомых строк равно (m * (m – 1)) mod 10⁹ + 7.

Пусть длина входной строки больше 2. На первой позиции может находиться любая из m букв, а на второй позиции – любая из m – 1 букв. Третья позиция должна отличаться от второй (вторая и третья буква не должны образовывать палиндром). Третья позиция должна отличаться от первой (первые три буквы не должны образовывать палиндром). Значит на третьей позиции может находиться любая из m – 2 букв.

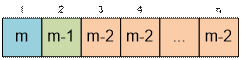
Следуя этой логике, заключаем что буква на i-ой позиции должна отличаться от букв на позициях (i – 1) и (i – 2). Количество искомых строк равно (m * (m – 1) * (m – 2)^{n – 2}) mod 10⁹ + 7.

Реализация алгоритма

Объявим модуль, по которому будут проходить вычисления.

#define MOD 1000000007

Функция powmod вычисляет значение xⁿ mod m.

long long powmod(long long x, long long n, long long m)

{

if (n == 0) return 1;

if (n % 2 == 0) return powmod((x * x) % m, n / 2, m);

return (x * powmod(x, n - 1, m)) % m;

}

Основная часть программы. Читаем входные данные.

scanf("%d", &tests);

while (tests--)

{

scanf("%lld %lld", &n, &m);

Вычисляем ответ в зависимости от значений n и m.

if (n == 1) res = m; else

if (m == 1) res = 0; else // n > 1, m = 1: aa....a

if (n == 2) res = (m * (m - 1)) % MOD; else

res = ((m * (m - 1)) % MOD * powmod(m - 2, n - 2, MOD)) % MOD;

Выводим ответ.

printf("%lld\n", res);

}